The centre of mass or mass centre is the mean location of all the massin a system. In the case of a rigid body, the position of the centre of mass is fixed in relation to the body. In the case of a loose distribution of masses in free space, such as shotfrom a shotgunor the planetsof the solar system, the position of the centre of mass is a point in space among them that may not correspond to the position of any individual mass.
The term centre of mass is often used interchangeably with centre of gravity, but they are physically different concepts. They happen to coincide in a uniform gravitational field, but where gravity is not uniform, centre of gravity refers to the mean location of the gravitational force acting on a body.
The centre of mass of a body does not generally coincide with its geometric centre, and this property can be exploited. Engineers try to design a sports car‘scentre of mass as low as possible to make the car handlebetter. When high jumpersperform a “Finsbury Flop“, they bend their body in such a way that it is possible for the jumper to clear the bar while his or her centre of mass does not.
CENTRE OF MASS OF A REGULAR OBJECT
If an object has uniform densitythen its centre of mass is the same as the centroidof its shape.
Examples:
· The centre of mass of a ring is at the centre of the ring (in the air).
· The centre of mass of a solid triangle lies on all three medians and therefore at the centroid, which is also the average of the three vertices.
· The centre of mass of a rectangle is at the intersection of the two diagonals.
· In a spherically symmetric body, the centre of mass is at the centre. This approximately applies to the Earth: the density varies considerably, but it mainly depends on depth and less on the latitudeand longitudecoordinates.
· More generally, for any symmetry of a body, its centre of mass will be a fixed point of that symmetry.
CENTRE OF MASS OF AN ARBITRARY 2D PHYSICAL SHAPE
The Centre of Mass of an arbitrary 2D physical shape can be found using the following plumbline method as illustrated in the following table:
|
|
|
|
|
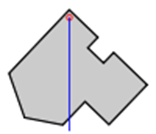
Step 1: An arbitrary 2D shape.
|
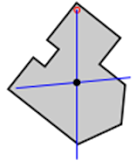
Step 2: Suspend the shape from a location near an edge. Drop a plumb line and mark on the object. |
Step 3: Suspend the shape from another location not too close to the first. Drop a plumb line again and mark. The intersection of the two lines is the centre of mass. |
Table 4.2: Centre of Mass of an arbitrary 2D physical shape
This method is useful when one wishes to find the centroidof a complex planar shape with unknown dimensions. It relies on finding the centre of mass of a thin body of homogenous densityhaving the same shape as the complex planar shape.
CENTRE OF MASS OF AN L-SHAPED OBJECT
This is a method of determining the centre of mass of an L-shaped object.
 |
| Centre of Mass of an L-shaped object |
1. Divide the shape into two rectangles, as shown in fig 2. Find the centre of masses of these two rectangles by drawing the diagonals. Draw a line joining the centres of mass. The centre of mass of the shape must lie on this line AB.
2. Divide the shape into two other rectangles, as shown in fig 3. Find the centres of mass of these two rectangles by drawing the diagonals. Draw a line joining the centres of mass. The centre of mass of the L-shape must lie on this line CD.
3. As the centre of mass of the shape must lie along AB and also along CD, it is obvious that it is at the intersection of these two lines; at O. (The point O may or may not lie inside the L-shaped object.)